SUPERPLASTICITÉ DES MÉTAUX

SUPERPLASTICITÉ DES MÉTAUX

L’une des propriétés principales de l’état métallique est l’aptitude à la déformation sous l’effet d’une contrainte. Selon la valeur de celle-ci, la déformation résultante peut être élastique , c’est-à-dire qu’elle se résorbe si la contrainte cesse d’être appliquée, ou plastique , le solide conservant dans ce cas une déformation permanente après que la sollicitation mécanique a été supprimée. On caractérise quantitativement la plasticité par l’aptitude d’un métal ou d’un alliage donné à tolérer sans se rompre une déformation plus ou moins importante. Cette propriété, qui tient à la nature de la liaison entre atomes constituant le solide métallique, est spécifique: les solides non métalliques (verres, céramiques, cristaux ioniques, polymères...) présentent une cohésion qui dépend de liaisons fondamentalement différentes. Ce fait a pour conséquence soit que ces matériaux n’ont pratiquement pas de plasticité, soit qu’ils sont doués d’une plus ou moins grande capacité de déformation, mais que leur résistance mécanique intrinsèque reste limitée. Par contre, les solides métalliques témoignent généralement à la fois d’une notable résistance et d’une capacité importante de déformation.

Zones de déformation

Les modes de sollicitation mécanique sont fort nombreux: traction, compression, flexion, torsion, cisaillement... Le plus commun et le plus simple consiste à appliquer une force de tension uniaxiale (essai de traction); il peut donc être considéré à titre d’exemple pour définir les principales caractéristiques du comportement mécanique d’un matériau métallique. On supposera, pour rester dans le cas le plus général, que le matériau considéré est polycristallin, c’est-à-dire constitué de la juxtaposition de grains (chacun d’eux étant un monocristal plus ou moins parfait) séparés par des frontières appelées joints de grains. La courbe de traction classique obtenue à partir d’une éprouvette polycristalline est du type de celle qui est représentée sur la figure 1. Les paramètres portés sur le graphe sont, en ordonnées, l’effort F appliqué ou contrainte apparente (S⁰ désignant la section droite initiale de l’éprouvette):

et, en abscisses, l’allongement résultant L ou déformation relative apparente:

si L⁰ désigne la longueur utile de l’éprouvette (généralement, il s’agit de la longueur entre congés raccordant le corps de l’éprouvette à ses têtes; on peut aussi bien considérer une longueur de base repérée initialement sur le corps de cette éprouvette).

Il faut distinguer sur la courbe trois zones, qui sont représentées sur la figure 1.

Zone I

La portion correspondant à la zone I de la courbe de traction est un segment de droite OA. La déformation est donc élastique, homogène et réversible; de plus, il y a proportionnalité entre les contraintes appliquées et les déformations élastiques résultantes. Le comportement élastique relève de la loi classique de Hooke:

E étant le module d’élasticité linéaire , ou module de Young, de valeur généralement élevée: les déformations élastiques sont donc faibles en valeur absolue.

L’ordonnée du point A définit la limite d’élasticité macroscopique 靖^E; la connaissance de cette valeur est fondamentale pour les calculs de résistance des matériaux. Lorsque le point A (ou limite de proportionnalité) est difficile à déterminer avec précision, on convient de mesurer ce que l’on appelle la limite d’élasticité macroscopique conventionnelle, soit la valeur de la contrainte entraînant une déformation permanente fixée arbitrairement (par exemple 﨎 = 0,2 p. 100, d’où la valeur 靖^E0,2).

Zone II

La portion correspondant à la zone II est un segment de courbe monotone AM à courbure non constante, le point M étant un extremum:

Dans ce domaine, la déformation est essentiellement plastique, homogène et non réversible; l’effort qu’il est nécessaire d’appliquer à l’éprouvette pour poursuivre sa déformation ne reste pas constant mais croît de façon continue: ce fait traduit le phénomène de consolidation.

Diverses caractéristiques importantes méritent d’être ici mentionnées:

– La contrainte apparente maximale atteinte (ordonnée du point M) est désignée par la terminologie de contrainte de rupture:

en dépit de ce vocable (d’ailleurs normalisé), on constate cependant que la rupture n’est pas encore survenue.

– Si l’on applique une contrainte intermédiaire entre 靖^E et 靖^R (point C, par exemple), la déformation totale produite (soit OC 﨎^T) est celle qui est mesurée sous contrainte. Si cette dernière est relâchée, on enregistre une décharge CC linéaire et sensiblement parallèle à OA; il en résulte que l’on récupère une déformation élastique C C = 﨎^e et que, par différence, on peut estimer la déformation plastique conférée de façon irréversible OC = 﨎^p . Notons incidemment que, si l’on recharge l’éprouvette, sa déformation est (sauf cas particulier) traduite par la droite CC (principe de Tresca), puis par la courbe CM (principe de Wiedemann): c’est-à-dire que la consolidation reprend au point C et non en tout autre point (ce fait n’est d’ailleurs pas toujours observé: phénomènes complexes de «vieillissement»).

– Les termes de «déformation homogène» précédemment utilisés traduisent spécifiquement le fait que toute la partie utile de l’éprouvette se déforme uniformément (fig. 2 a, 廓); on peut donc également mesurer l’allongement plastique uniformément réparti OM = 﨎^M.

Zone III

La portion de courbe correspondant à la zone III est le segment MD à courbure non constante. Dans ce domaine, la déformation demeure essentiellement plastique et irréversible , mais elle est cette fois hétérogène : de fait, il y a striction et la section cesse d’être uniforme sur toute la longueur utile (fig. 2 a, 塚 et 嗀), l’effort exercé diminuant au fur et à mesure que l’allongement croît. Finalement, la striction est interrompue au moment de la rupture de l’éprouvette (point D, fig. 1). Selon les cas, le domaine de striction peut être étendu ou restreint, voire inexistant, ce qui signifie alors que le matériau est fragile. On caractérise également le comportement d’un matériau en indiquant l’allongement plastique acquis au moment de la rupture, soit: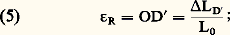

cette valeur traduit également la ductilité du matériau, qui reste le plus souvent inférieure à 100 p. 100.

On remarquera que le domaine de striction débute à partir du point M pour lequel la tangente est horizontale. Le fait que la déformation plastique se poursuive au-delà de M, bien que la charge appliquée diminue, prouve qu’il se produit un phénomène dit d’instabilité géométrique ; au point M, la relation suivante est vérifiée:

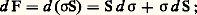le premier terme S d 靖 traduit le phénomène de consolidation (d 靖 礪 0), tandis que le second rend compte de la diminution de charge liée à la réduction progressive de section (d S 麗 0). On conçoit donc que les deux termes puissent se compenser à un instant donné; l’effort appliqué passera par un maximum, tandis que la contrainte continuera de croître dans la section la plus réduite de l’éprouvette.

Enfin, après rupture, la section rompue aura une aire S^f et on définira la striction par la relation:

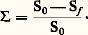Analyse du phénomène de plasticité

Jusqu’à présent, seuls ont été mentionnés les paramètres apparents 靖^a (lié à S⁰) et 﨎^a (lié à L⁰). En réalité, en un point donné du domaine plastique (zone II, fig. 1), la section réelle est S et la longueur utile de l’éprouvette est devenue égale à L. Il paraît donc plus correct de définir de nouveaux paramètres, qui sont la contrainte vraie instantanée et la déformation relative vraie instantanée, respectivement:

dont les valeurs 靖v et 﨎v sont dites rationnelles ; on montre facilement que:

Ces formules ne sont valables que pour la suite de la courbe de traction située dans la zone II.

L’analyse mathématique de la courbe de consolidation (segment AM, fig. 1) montre que l’équation proposée par Ludwick dès 1909 est souvent vérifiée, soit: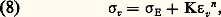

dans laquelle K est une constante et n le coefficient de consolidation . Il y a lieu de ne pas confondre n avec ce que l’on appelle le taux de consolidation :

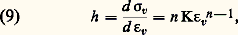qui n’est autre que la pente en un point donné de la courbe de consolidation en coordonnées rationnelles .

Le coefficient de consolidation peut être déterminé de diverses façons; l’une d’elles dérive directement de la relation (8); il suffit en effet de mesurer la pente de la droite obtenue en portant ln 靖v en fonction de ln 﨎v, soit encore:

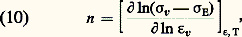où 﨎 est défini dans la relation (12).

La seconde méthode est fondée sur une relation simple que l’on peut déduire du critère d’instabilité géométrique. En effet, appelons 靖^s et 﨎^s la contrainte et l’allongement rationnels correspondant au début de striction. On doit avoir d F = 0, soit:

ou encore, en tenant compte de la relation (8):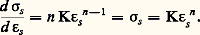

Finalement:

Les considérations précédentes ne font intervenir que les paramètres mesurés expérimentalement dans des conditions d’essais données, en particulier pour une température et une vitesse de traction fixées à l’avance. En fait, ces deux variables exercent une influence marquée sur l’allure de la courbe de traction. Par définition, la vitesse de traction (qu’il est relativement aisé de maintenir constante durant l’essai) s’exprime conventionnellement par: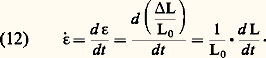

On peut définir de façon similaire une vitesse de déformation :

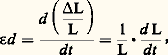mais on se rend facilement compte qu’il ne suffit pas de maintenir constante la vitesse de traction pour avoir 﨎^d invariante.

Une relation traduisant l’influence de la vitesse de traction a été proposée par Carreker et Hibbard:

à température donnée, dans laquelle A est une constante caractéristique du matériau et m le coefficient de sensibilité à la vitesse . On peut donc évaluer ce coefficient à partir de la relation: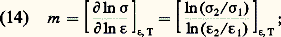

plus la valeur de m est grande (m 礪 0,3), plus la déformation s’opère dans des conditions proches de celles de l’écoulement visqueux de type newtonien, pour lequel m = 1.

Aucune loi simple n’a été trouvée à ce jour pour traduire l’influence de la température; on peut cependant schématiser, dans le cas général, le rôle de ce paramètre par deux caractéristiques essentielles: en fonction de la température croissante, on observe une chute de plus en plus notable de la limite d’élasticité ainsi que de la charge à la rupture, tandis que la ductilité augmente. Toutefois, certaines exceptions sont constatées dans le cas d’alliages au sein desquels, dans des intervalles donnés de températures, il peut se produire à chaud des interactions entre les atomes de soluté et les défauts linéaires (dislocations) distribués au sein du matériau (par exemple phénomène Portevin-Le Chatelier).

En dernier lieu, il convient de signaler que l’analyse approfondie des phénomènes dans le cas plus simple des monocristaux a permis d’établir qu’en réalité la consolidation s’opérait en plusieurs stades (en général trois), comme le montrent les courbes de la figure 3. On constate en fait que la symétrie cristalline exerce un rôle prépondérant; dans le cas des cristaux de symétrie cubique à faces centrées ou de symétrie hexagonale compacte (courbes 1 et 2), l’allure des portions de courbes correspondant respectivement aux divers stades est similaire; cependant, les caractéristiques majeures (étendue des divers domaines et pentes des segments linéaires) ont des valeurs assez différentes. On est convenu de distinguer ainsi:

– stade I: glissement facile;

– stade II: consolidation linéaire;

– stade III: consolidation parabolique.

Dans le cas des cristaux de symétrie cubique centrée (courbe 3), la différence essentielle réside dans le fait que le stade I correspond à une consolidation parabolique. Les courbes 1 , 2 et 3 traduisent l’évolution qui se produit lorsque la température d’essai diminue.

Mécanismes contrôlant la plasticité

Dans les matériaux monocristallins ou polycristallins, la déformation plastique s’effectue essentiellement par glissement; c’est lorsque ce mécanisme est défavorisé que le processus de maclage intervient. Enfin, dans certaines conditions particulières, on peut observer un glissement visqueux intergranulaire ou un microfluage contrôlé par la diffusion.

Glissement

Dans le cas du glissement, certaines parties d’un cristal sont déplacées par translation uniforme relative, parallèlement à des directions cristallographiques denses, les directions de glissement (fig. 4).

Les plans séparant les régions ayant subi ce déplacement relatif sont dits plans de glissement. Selon l’importance de la déformation atteinte, le déchaussement créé s’amplifie et on observe sur la surface du cristal déformé soit des lignes de glissement fines ( 﨎 麗 10 p. 100), soit des bandes de glissement épaisses ( 﨎 礪 10 p. 100), constituées de lamelles ayant glissé les unes par rapport aux autres comme les cartes d’un jeu. Il faut souligner que, dans ce mode de déformation, il n’y a pas modification de l’orientation cristalline, quelle que soit la région considérée.

Le glissement peut être simple (un seul plan de glissement actif) ou multiple (plusieurs plans de glissement conjointement ou sucessivement actifs, ces plans appartenant à une même famille de plans cristallographiques ou à des familles différentes). À l’échelle microscopique, le glissement résulte du déplacement de défauts linéaires: dislocations coin ou vis dans leur plan de coupure. Les dislocations vis peuvent également changer de plan de déplacement dans la mesure où les deux plans successivement balayés admettent une intersection parallèle à la direction de glissement: cas du glissement dévié .

De plus, le glissement aurait tendance à engendrer un déplacement relatif des extrémités du cristal ainsi déformé (fig. 4 a); ce déplacement étant empêché par le fait que la direction de l’effort appliqué reste invariante, il se produit des hétérogénéités d’accommodation dénommées pliages , qui correspondent à des rotations locales du réseau, sans intervention de glissement secondaire, du moins à l’origine (fig. 4 b).

Maclage

Certaines régions d’un cristal subissent un cisaillement homogène parallèlement à un plan (plan de maclage) et à une direction contenue dans ce plan (direction de maclage). Une coupe du cristal ainsi déformé, par un plan perpendiculaire au plan de maclage, permet de montrer que la disposition des atomes dans la zone maclée est devenue symétrique de celle qui est observée dans la matrice initiale non maclée (fig. 5).

Il y a donc modification locale de l’orientation, mais la structure cristalline reste toutefois inchangée. Le maclage est généralement favorisé par des contraintes élevées et des températures basses.

Glissement intergranulaire et microfluage diffusionnel

À température élevée (voisine de la température de fusion) et pour des contraintes appliquées relativement faibles, la déformation plastique est susceptible de s’effectuer selon deux nouveaux modes.

– Les grains se déplacent progressivement les uns par rapport aux autres le long de leurs frontières communes (joints). Leur mouvement relatif est le plus important lorsque les joints sont disposés à 45⁰ de la direction de l’effort appliqué: ce phénomène est aisément mis en évidence par mesure des décalages créés sur des lignes repères primitivement tracées sur la surface du matériau. La déformation est cependant très difficile aux intersections des joints, et des déchaussements apparaissent. Le phénomène peut s’interpréter par un écoulement quasi visqueux sur les surfaces intergranulaires; cependant, sa contribution à la déformation totale d’une éprouvette reste inférieure à 30 p. 100.

– À température élevée, la concentration d’équilibre des défauts ponctuels (lacunes) est importante; leur mobilité est également notable. Dans ces conditions, la déformation plastique peut se produire par microfluage diffusionnel. De fait, C. Herring et F. R. N. Nabarro ont proposé un modèle selon lequel les lacunes migrent alors vers les joints de grains disposés parallèlement à la direction de l’effort appliqué; ce flux de lacunes est compensé par un flux antagoniste d’atomes vers les joints placés normalement à la direction de l’effort. Il en résulte une évolution de la morphologie des grains qui s’allongent dans la direction de la contrainte appliquée et se rétrécissent dans la direction transverse, ce qui justifie la déformation produite. On constate le plus souvent que la vitesse de déformation résultante est proportionnelle à la contrainte exercée; le processus est donc macroscopiquement analogue à un écoulement visqueux (de type newtonien) intragranulaire: voir équation (13) avec m = 1.

Superductilité et superplasticité

Certains matériaux sont susceptibles, sous l’effet d’une contrainte relativement faible, de se déformer de manière extensive avant de se rompre: alors que la ductilité classique des matériaux métalliques reste inférieure à 100 p. 100, on observe dans certains cas des allongements de l’ordre de 1 000 à 2 000 p. 100 (soit vingt fois la longueur primitive). Plus précisément l’instabilité géométrique qui se manifeste de façon aléatoire en une zone de l’éprouvette donne alors lieu à un allongement régulier très important par simple étirement du faible étranglement initialement apparu; il n’y a plus localisation de la déformation comme dans la striction classique (fig. 2 b).

Le terme de superplasticité n’a été proposé qu’en 1945 par A. A. Bochvar pour caractériser les phénomènes singuliers (du type de ceux qui viennent d’être évoqués) observés dans certaines conditions opératoires avec les alliages Zn-Al. Cependant, bien des années auparavant, de nombreux chercheurs avaient signalé à diverses reprises des comportements plastiques anormaux. En raison de cette similitude apparente de l’aptitude à l’ultradéformation, une certaine confusion a régné, alors que les causes motivant les possibilités d’allongement anormal étaient fondamentalement différentes. Il est donc nécessaire de bien distinguer entre phénomènes de ductilité exagérée (ou superductilité) et de superplasticité .

Comme l’indique la terminologie de ductilité exagérée, il s’agit de phénomènes se traduisant par un simple accroissement de la capacité normale de déformation d’un matériau donné, le plus souvent du simple au double, voire exceptionnellement au triple. On peut regrouper les divers exemples signalés en quatre cas principaux:

– Ductilité exagérée résultant d’une déformation mécanique effectuée pendant une transformation allotropique se développant à température élevée. Dès 1924, A. Sauveur a signalé que, par torsion d’une barre de fer chauffée dans un gradient longitudinal de température, on provoque une déformation considérable dans la partie de la barre où coexistent les phases 見 et 塚. Ces faits ont été confirmés de façon plus précise par divers auteurs, aussi bien sur le matériau précité que sur d’autres métaux susceptibles d’allotropie, par exemple l’uranium ou le zirconium.

– Ductilité exagérée résultant d’une déformation mécanique effectuée pendant une transformation structurale à température moyenne ou peu élevée. L. F. Porter et P. C. Rosenthal ont en particulier analysé ce genre de phénomènes sur un acier à teneur eutectoïde, sollicité mécaniquement durant les transformations de type perlitique, bainitique ou martensitique. Des conclusions similaires ont été mentionnées pour des aciers plus complexes, contenant en particulier du chrome.

– Ductilité exagérée observée en fluage. Différents auteurs ont en effet noté la possibilité d’augmentation anormale de la déformation par fluage sous contrainte uniaxiale de tension, à température relativement élevée. Les causes alors invoquées sont le plus souvent soit un processus de recristallisation intervenant durant l’essai proprement dit, soit une variation de la solubilité d’un constituant permettant de former ou de détruire temporairement l’une des phases présentes dans l’alliage polyphasé soumis à l’essai de fluage.

– Ductilité exagérée développée par écrouissage. Certains matériaux comme le magnésium et ses alliages, qui n’ont normalement qu’une capacité très limitée de déformation en traction à température ordinaire, peuvent acquérir un allongement à rupture très largement supérieur s’ils ont été soumis au préalable à un filage-étirage ou à des laminages successifs «à tiède», puis à froid. Le phénomène de ductilité exagérée constaté ensuite lors d’essais mécaniques classiques a été attribué à l’existence de zones très «cisaillées» lors de la mise en forme préalable; ultérieurement, un écoulement quasi visqueux peut se produire dans ces zones sous l’action de la contrainte appliquée durant l’essai de traction final.

Par opposition, un comportement superplastique conduira à des possibilités de déformation pouvant être dix fois plus grandes que celles qui traduisent la superductilité. Les premiers exemples effectifs d’un tel comportement ont été décrits par C. E. Pearson, qui a montré en 1934 la possibilité de déformation plastique sans striction atteignant jusqu’à 2 000 p. 100 dans le cas des alliages Pb-Sn et Bi-Sn. Une dizaine d’années plus tard, A. A. Bochvar a observé des phénomènes similaires avec les alliages Zn-Al: cette étude a été suivie de nombreux travaux réalisés en Union soviétique par A. A. Presnyakov et ses collaborateurs entre 1958 et 1963 sur des alliages d’aluminium ainsi que sur des laitons. De nombreuses études ont également été effectuées aux États-Unis, en particulier par W. A. Backofen et D. H. Avery sur les alliages Zn-Al et Pb-Sn, ainsi que par T. H. Alden sur un alliage Sn-Bi.

Caractéristiques du phénomène de superplasticité

Influence de la valeur d’un coefficient de sensibilité à la vitesse

Si l’on regroupe les expressions (8) et (13), on peut définir une pseudo-équation d’état mécanique:

de laquelle on déduit:

La contrainte vraie qui provoque la déformation est donc fonction de la déformation déjà conférée et de la vitesse de déformation. Dans le cas des matériaux classiques, ou pour les matériaux superplastiques hors de leur domaine de superplasticité, les deux termes du second membre de l’équation (16) peuvent exercer des effets comparables: en effet, on a alors n 諒 0,3 et m 諒 0,2.

Au contraire, dans le cas des matériaux présentant un comportement superplastique, n est très faible tandis que m est le plus souvent compris entre 0,5 et 1 (du moins, dans un certain domaine de vitesses de déformation).

Ces résultats sont schématisés par les courbes de la figure 6, dans laquelle on notera en particulier l’aspect sigmoïde caractéristique de la courbe 廓 (fig. 6 a) correspondant aux matériaux superplastiques, ainsi que l’existence d’un extremum dans la courbe 廓 (fig. 6 b), de part et d’autre duquel s’étend le domaine de superplasticité.

Par suite, la caractéristique essentielle de l’état superplastique est que le coefficient de sensibilité à la vitesse présente une valeur élevée; d’autre part, cette condition n’est satisfaite que dans une gamme critique de vitesses de déformation.

Une valeur élevée de m justifie-t-elle à elle seule un comportement superplastique? De fait, à partir des équations (6) et (13), on peut écrire: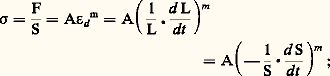

d’où: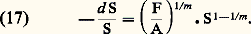

Donc, si m = 1, la réduction progressive de section est indépendante de S, de sorte que la poursuite de la déformation n’a pas tendance à créer une striction locale, et l’écoulement demeure stable: autrement dit, un étranglement fortuit sera simplement étiré et ne s’accusera pas de façon catastrophique.

Au contraire, si m est faible (m 廉 1), la vitesse de réduction locale de la section (dans la zone de striction) augmente très vite au fur et à mesure que S diminue, et l’écoulement devient instable.

Comme l’a montré C. Rossard, l’écoulement stable superplastique peut, en pratique, être observé pour des valeurs m 閭 1/2 ou m 閭 1/3, selon que l’on opère respectivement à vitesse de traction ou à vitesse de déformation constante.

Dans ce contexte, un dernier point important est à signaler: du fait de la stabilité de l’écoulement en superplasticité, les anomalies constitutionnelles (irrégularité de surface, fissures, microcavités...) n’exercent pas ces effets souvent catastrophiques que l’on observe dans le cas des matériaux classiques, qui se traduisent par une chute de ductilité ou conduisent à des ruptures prématurées.

Influence de l’état structural du matériau

Les matériaux cristallins qui présentent un comportement superplastique sont assez nombreux: le tableau en donne quelques exemples. Ils ne sont capables de ce comportement que s’ils présentent naturellement, ou si on leur confère volontairement, une structure micrographique singulière par un traitement thermique convenable. Cette structure est constituée de grains équiaxes très petits (de l’ordre du micromètre) appartenant à deux phases distinctes, dont la ductilité propre est similaire et dont les proportions relatives sont sensiblement du même ordre. Les structures à grains très fins sont éminemment instables dans le cas des métaux purs; par suite, les matériaux superplastiques sont nécessairement des alliages, le plus souvent de nature eutectique ou eutectoïde. La stabilité structurale de ces structures fines polyphasées est donc liée au phénomène d’inhibition de croissance qu’exercent les petits grains de l’une des phases en présence sur les cristaux de l’autre, et réciproquement. Cette stabilité demeure même par maintien à température supérieure à 0,5 T^f et quelle que soit la déformation conférée. De fait, si l’on effectue, par exemple, une déformation par traction sur un matériau à comportement classique, on observe, entre autres phénomènes, une élongation progressive des grains dans la direction de la contrainte appliquée; au contraire, dans un matériau à comportement superplastique, l’évolution de la taille et de la morphologie des grains est pratiquement négligeable.

Par ailleurs, les examens en transmission au microscope électronique, sur lames minces prélevées dans les matériaux superplastiques, ne mettent pas en évidence la présence de dislocations, ni avant ni après déformation; au contraire, la consolidation des matériaux à comportement classique se traduit par une multiplication très notable des défauts linéaires.

Enfin, la valeur moyenne de la dimension des grains influe sur les caractéristiques considérées précédemment. En effet, une augmentation de la taille des grains entraîne un déplacement significatif des courbes 廓 et 廓 de la figure 6 vers les faibles vitesses de déformation. Un exemple concret en est donné sur la figure 7.

Influence de la température

De façon schématique, pour un matériau susceptible d’un comportement superplastique, il est admis que le phénomène ne se manifeste qu’au-delà d’une température supérieure à une valeur critique, de l’ordre de la moitié de la température de fusion. On peut toutefois être plus explicite en distinguant les deux effets principaux qu’exerce la température; cela peut être illustré en prenant comme exemple l’alliage monotectoïde 78 ZN-22 Al, dont le palier invariant est situé à 275 ⁰C:

– si l’alliage est trempé depuis une température supérieure à celle du palier, il présente le phénomène de superplasticité; en revanche, il n’est plus superplastique si l’homogénéisation, suivie de trempe et d’un refroidissement, a été effectuée à une température inférieure à 275 ⁰C;

– dans le cas où le comportement superplastique est observé, l’allongement réalisé est maximal si la température de déformation est aussi voisine que possible de celle du palier invariant (tout en lui restant inférieure).

Mécanismes proposés pour rendre compte du phénomène

Différents modèles ont été proposés, dont aucun n’est parfaitement satisfaisant. Il a d’abord été suggéré d’étendre au cas de la superplasticité les mécanismes proposés pour rendre compte du fluage à température relativement élevée et sous faible contrainte appliquée. Ces mécanismes sont essentiellement fondés sur l’hypothèse que les défauts ponctuels (lacunes) migrent de façon préférentielle lorsqu’une contrainte uniaxiale est imposée: ils ont déjà été évoqués précédemment.

Dans le présent contexte, les formulations mathématiques que l’on peut déduire sont les suivantes:

selon que les déplacements préférentiels s’opèrent au travers du réseau ou le long des points de grains. Dans ces expressions: d désigne la dimension moyenne des grains D^v et D^j les coefficients de diffusion en volume ou aux joints, 行 le volume atomique, 靖 la contrainte appliquée, k la constante de Boltzmann, T la température d’essai (kelvins) et 嗀^j la largeur moyenne des joints de grain.

Elles traduisent une relation linéaire entre 﨎 et 靖, soit m = 1, or l’expérience révèle que ce coefficient est plus ou moins inférieur à l’unité. Par ailleurs, les processus invoqués conduisent à une élongation des cristaux lorsque l’allongement de l’éprouvette se développe, ce qui n’est pas observé expérimentalement en déformation superplastique.

D’autres auteurs ont alors suggéré qu’il était plus vraisemblable de combiner les mécanismes précédents, n’impliquant que les défauts ponctuels, avec des processus mettant en jeu la mobilité des défauts linéaires (dislocations) soit par glissement dans le plan de coupure, soit par montée hors de ce plan. Ainsi D. H. Avery et W. A. Backofen ont proposé une équation du type: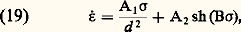

A³, A⁴ et B étant des constantes.

Sur les mêmes bases, mais en incorporant le formalisme de Weertman, C. M. Packer et O. D. Sherby ont abouti à une expression plus compliquée:

A³, A⁴ et B¹ étant des constantes.

Partant de l’idée que les limites intergranulaires sont des régions assez désordonnées et, par là même, analogues à un fluide quasi visqueux, T. H. Alden a suggéré que la superplasticité pouvait être expliquée par le déplacement des grains les uns par rapport aux autres, la succession des glissements relatifs des grains des deux phases en présence rendant compte de l’allongement progressif de l’échantillon. De fait, cet auteur a expérimentalement observé que les lignes repères tracées sur la surface présentaient, après déformation, des continuités aux joints. Cependant, il n’a pas justifié le fait que de tels glissements intergranulaires n’engendrent pas la formation de cavités intergranulaires; il n’a pas d’ailleurs donné la raison pour laquelle les points triples n’inhibent pas le processus.

Enfin, une dernière hypothèse fait appel à un mécanisme de restauration dynamique. Il est en effet connu que, lors d’un corroyage des matériaux métalliques à température suffisamment élevée, il se produit une recristallisation en même temps que la déformation s’effectue. Packer, Johnson et Sherby ont alors indiqué un modèle selon lequel la contrainte appliquée crée d’abord une distorsion locale du réseau par glissement classique au voisinage des joints. Compte tenu de la température relativement élevée à laquelle s’effectue la déformation, ces régions pertubées recristallisent: cela se traduirait en fait par une migration à courte distance des joints de grain (ne modifiant cependant pas en moyenne la dimension des cristaux, mais pouvant justifier la faible évolution de morphologie des grains qui a été observée: contours devenant émoussés ou arrondis). Ce modèle justifie que le matériau ne se consolide pas, l’adoucissement induit par la restauration dynamique maintenant la ductilité. L’explicitation mathématique entraîne seulement une modification du premier terme de l’équation (20).

Ce bref aperçu des théories suggérées confirme bien que l’interprétation détaillée du phénomène est loin d’être établie; cependant, on peut résumer brièvement l’idée générale que l’on s’en fait actuellement. Il ne s’agit plus de tenter uniquement de justifier le comportement superplastique, mais plutôt de montrer qu’il représente un type d’évolution intermédiaire entre deux comportements classiques: en fait, il s’agit de rendre compte de la forme en S caractéristique de la courbe ln 靖 = f (ln 﨎). Sur le schéma de la figure 8, cette courbe a été divisée en trois parties:

– La première correspond aux faibles vitesses 﨎; les valeurs de m sont basses (face=F0019 力 0,2); les allongements qu’il est possible de développer sont limités et la forme des grains demeure rigoureusement inaltérée après déformation (contours anguleux, grains étroitement imbriqués se verrouillant les uns les autres). L’hypothèse de Backofen est que la faible valeur de m résulte de l’existence d’une «contrainte de retour» 靖⁰ s’opposant à la contrainte appliquée 靖, de sorte que la contrainte d’écoulement efficace ne serait plus égale qu’à ( 靖 漣 靖⁰).

– La deuxième partie correspond à des valeurs intermédiaires de 﨎; on obtient m 閭 0,5; le comportement est alors typiquement superplastique, tandis que les contours de grains tendent à devenir curvilignes, d’où une morphologie arrondie des grains, de dimensions par ailleurs pratiquement invariantes. Il se produit une relaxation aux joints (recristallisation locale), vraisemblablement concomitante d’un glissement visqueux (sans création de cavités).

– Une dernière partie correspond aux fortes vitesses de déformation; le coefficient m redevient faible (m 力 0,3), les allongements régressent sensiblement, tandis que les grains s’allongent nettement dans la direction de la contrainte appliquée. Le processus mis en jeu dans de telles conditions est un fluage classique intragranulaire.

Les mêmes observations peuvent être déduites de la figure 7, combinant les valeurs de m , 﨎 et A p. 100.

Applications suggérées

Le phénomène de superplasticité développé dans le cas des matériaux à grains fins a déjà donné lieu à des applications en ce qui concerne leur mise en forme; les trois principaux domaines concernés sont le façonnage des tôles, le tréfilage sans filière et l’amélioration des opérations classiques telles que le laminage, le forgeage ou l’extrusion.

Depuis 1964, on façonne des tôles d’alliages superplastiques soit par aspiration sous vide, soit par application de pressions gazeuses de l’ordre de celles qui sont utilisées en thermoplastie. Le mode opératoire est simple: il suffit de pincer la périphérie du flan, qui est ensuite chauffé par radiation, induction ou effet Joule; une fois la température optimale atteinte, on aspire l’air qui se trouve emmagasiné entre le flan et les parois du moule (technique décrite en particulier par Fields) ou on injecte de l’air comprimé sous la tôle de façon qu’elle s’applique contre le moule (technique exploitée en premier lieu par Backofen, Turner ou Avery pour élaborer des dômes à parois minces). Des panneaux de portes intérieures de voitures ou de réfrigérateurs ont été ainsi réalisés en une seule opération à partir de tôles d’alliage Zn-22 Al (Prestal), portées à 260 ⁰C sous des pressions de l’ordre de 300 kN . m^-2. Des maquettes de carrosserie d’automobile ont également été moulées de la sorte. Cette technique de mise en forme présente de nombreux avantages:

– des pièces plus grandes et plus complexes peuvent être façonnées avec précision, ce qui réduit le nombre d’installations et les opérations d’assemblage ultérieures;

– l’usure des outils et la main-d’œuvre sont minimisées;

– il n’y a pas de problème de soudure ni de peinture;

– les traitements thermiques de parachèvement sont supprimés ou simplifiés;

– la tenue mécanique peut être rendue similaire à celle d’une construction en acier en augmentant légèrement les sections, ce qui n’accroît pas la masse globale, compte tenu de la masse volumique inférieure de l’alliage (par rapport à celles des aciers classiques).

Cependant, le matériau de base est plus onéreux; par ailleurs, les temps de mise en forme sont plus longs (le plus souvent de quelques minutes): pour conserver une bonne cadence de production, il faut donc envisager de multiplier les postes. Enfin, un façonnage à température supérieure à la température ambiante est plus coûteux.

En 1969, L. H. Johnson a proposé un procédé original, dit le tréfilage sans filière, qui permet d’obtenir par étirement des barres ou des tubes (fig. 9). Une pièce cylindrique est amarrée à l’une de ses extrémités, tandis que l’autre est déplacée à une vitesse V¹. Elle est par ailleurs chauffée à partir d’un inducteur qui se meut en sens inverse à la vitesse V²; le chauffage est réglé de telle sorte que le matériau soit localement porté à une température le rendant superplastique. En choisissant convenablement les valeurs du rapport V¹/V², on peut obtenir des taux de réduction 精 très élevés: ainsi, pour V¹/V² = 5, 精 力 83 p. 100 (allongement de 500 p. 100); on peut également faire varier V¹/V² au cours de l’opération et ainsi obtenir des barres à section variable. Cette technique a été appliquée à certains alliages de titane (Ti-6 Al-4 V) utilisés en aéronautique.

Enfin, on peut tirer parti du phénomène de superplasticité pour faciliter notablement certaines opérations de mise en forme telles que le laminage. Classiquement, il faut en effet mettre en œuvre des appareils importants, résistants et coûteux. On réduit substantiellement les efforts nécessaires en réalisant transitoirement un état superplastique. Par exemple, cela a été démontré par Hayden sur des alliages nickel-chrome à grains très fins. On confère des propriétés mécaniques plus intéressantes pour l’utilisation pratique en effectuant un traitement thermique ultérieur qui fait légèrement grossir les grains.

En dehors des considérations économiques et des difficultés techniques de mise au point de procédés industriels, le facteur essentiel qui limite encore le développement des matériaux superplastiques est l’amélioration de leurs caractéristiques à la température d’utilisation. Ainsi, bien que le Prestal, par exemple, se situe actuellement entre l’acier et les polymères, des études récentes ont déjà montré que de faibles additions (inférieures à 1 p. 100 de cuivre) étaient susceptibles d’augmenter significativement la résistance au fluage ainsi que les caractéristiques mécaniques.

Encyclopédie Universelle. 2012.